Úloha materiálové nelinearity je taková úloha, při které dojde vlivem zatížení ke vzniku plastické (trvalé) deformace. Tento typ numerické analýzy již nelze v NX Nastran řešit pomocí řešiče pro lineární statiku (SOL 101), ale je nutné zvolit řešič pro nelineární statiku (SOL 106). Z pohledu materiálového modelu je pak nutná znalost tahového diagramu pro použitý materiál.
Tento typ úlohy je vhodné použít vždy, když chceme znát hodnotu maximálního napětí nebo skutečné deformace a při použití SOL 101 je překročena mez kluzu pro daný materiál.
Úloha lineární statiky (SOL 101)

Ukázkovou úlohu ocelového pásku s otvorem namáhaného na tah nejprve vyřešíme pomocí řešiče NX Nastran pro lineární statiku (SOL 101) používaného pro řešení všech úloh v předmětu ICB.
Je potřeba uvažovat dostatečně velké zatížení, tak aby došlo k překročení meze kluzu materiálu. Pro náš případ budeme uvažovat teoretický materiál s mezí kluzu 300 MPa při poměrné deformaci 0,01 a s mezí pevnosti 500 MPa při poměrné deformaci 0,1. Zatěžující síla musí tedy při výpočtu úlohy lineární statiky vyvodit v pásku napětí vyšší než 300 MPa.
Jako vzorek pro tahovou zkoušku je použit 6 mm tlustý ocelový pásek o rozměrech 200x40 mm. Tento pásek má uprostřed otvor o průměru 25 mm.
Výpočtový model a okrajové podmínky
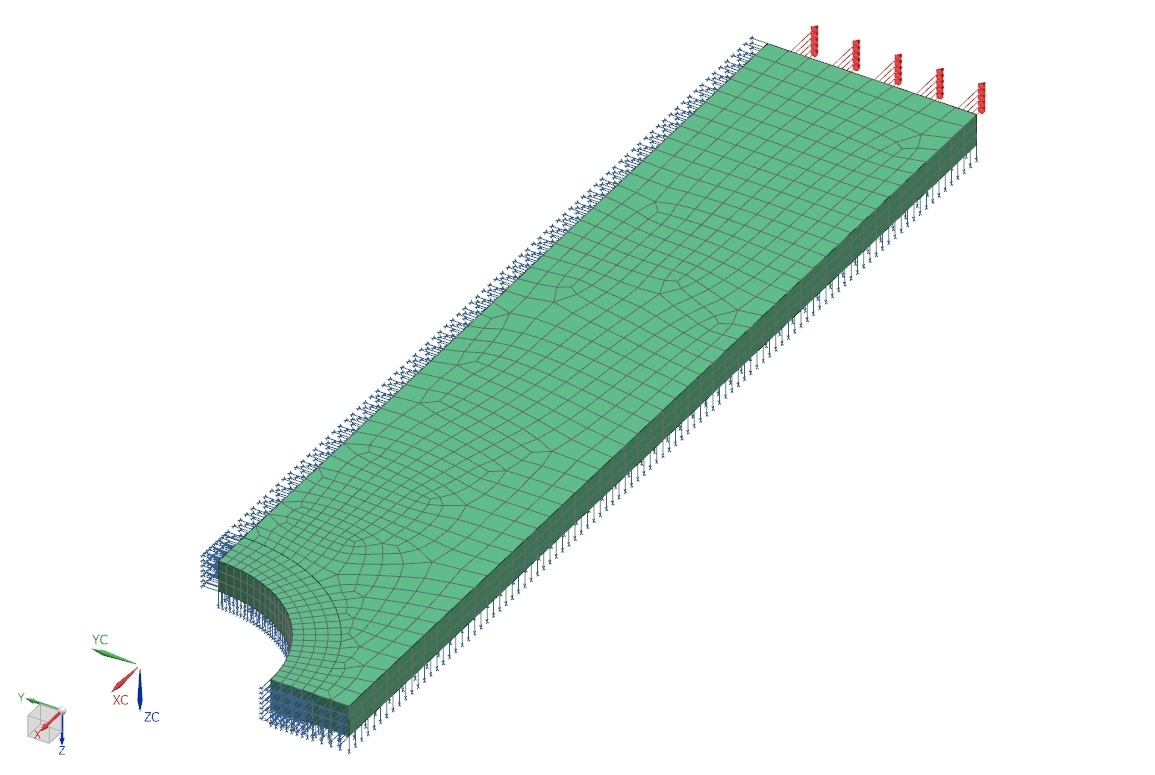
Vzhledem k tomu, že je model symetrický podle tří rovin, je pro výpočtový model možné použít pouze jednu osminu geometrie modelu s uvažováním okrajových podmínek symetrie v příslušných rovinách. V oblasti otvoru, kde předpokládáme výskyt nejvyššího napětí, je vhodné těleso rozříznout a použít 3D mapovanou síť.
Pro výpočet použijeme izotropní materiál s modulem pružnosti 210 000 MPa a Poissonovo číslem 0,27. Zadání těchto dvou konstant je pro úlohu lineární statiky dostačující.
Na všechny roviny symetrie aplikujeme příslušné okrajové podmínky symetrie zajišťující neproniknutí modelu do roviny symetrie. Na koncovou plochu aplikujeme zatížení ve formě síly o velikosti 7500 N (1/4 celkové síly 30 kN).
Výsledky úlohy lineární statiky
Z výsledků úlohy lineární statiky je patrné, že celková deformace vzorku je 0,078 mm a maximální redukované napětí je 707 MPa. Podle výpočtu tedy součást pro toto zatížení trvale pevnostně nevyhovuje, protože překračuje nejen mez kluzu (300 MPa) ale i mez pevnosti materiálu (500 MPa). Výpočet lineární statiky nám však nedokáže odpovědět na otázku, zda součást při jednorázovém zatížení touto silou praskne.


Úloha nelineární statiky (SOL 106)
Základním předpokladem pro řešení úlohy nelineární statiky s uvažováním materiálové nelinearity je znalost tahového diagramu pro použitý materiál. Pro výpočet můžeme použít stejný výpočtový model a stejné okrajové podmínky, ale musíme doplnit informace zadané v materiálovém modelu.
Definice materiálu
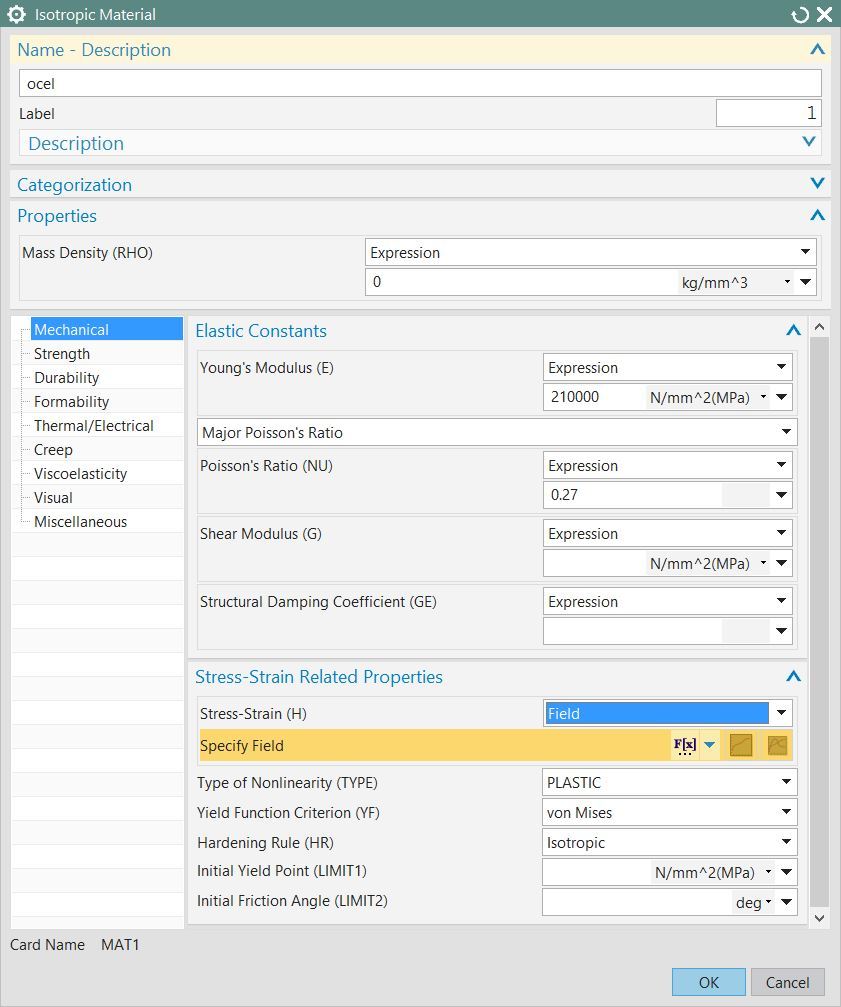
Místo výběru z knihovny vytvoříme pomocí ikony v pravém dolním rohu knihovny materiálů nový izotropní materiál. Budeme nastavovat hodnoty z oblasti mechanických vlastností (záložka Mechanical).
Je nutné zadat alespoň dvě ze tří elastických konstant. Naše hodnoty jsou 210 000 MPa pro modul pružnosti v tahu (Young´s Modulus) a 0,27 pro Poissonovo číslo. Modul pružnosti ve smyku (Shear Modulus) se dopočte automaticky dle závislosti pro izotropní materiál.
Takto zadaný materiál může být použit pro řešení úlohy lineární statiky bez uvažování vlastní hmotnosti (není definována hustota materiálu).
Pro řešení úlohy s materiálovou nelinearitou musíme definovat závislost napětí na poměrné deformaci (Stress-Strain) pomocí volby Field a výběru Table v políčku Specify Field.
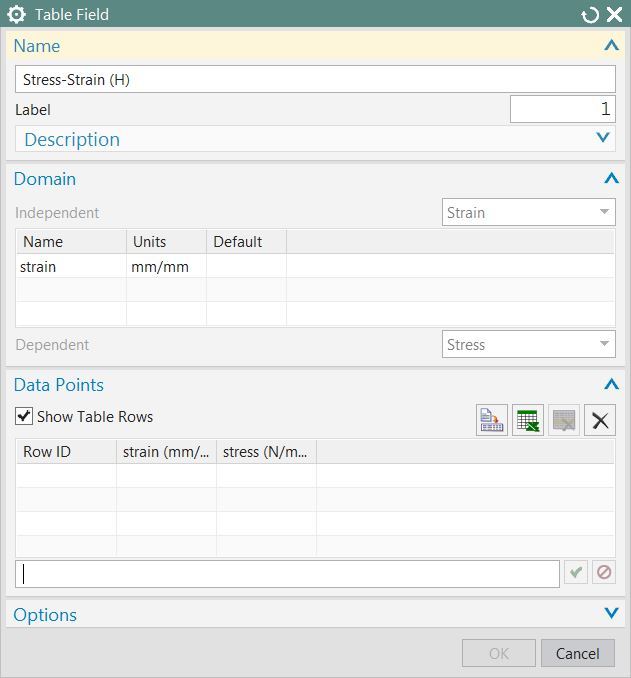
Definice Stress-Strain tabulky
Při definici nové Stress-Strain tabulky je nutné vybrat v záložce Domain v políčku Independent hodnotu Strain. Jednotlivé hodnoty se zadávají v záložce Data Points ve formátu strain,stress (např. 0,0 pro výchozí bod).
Pro naši úlohu použijeme zjednodušený bilineární diagram, který se skládá ze třech bodů:
- počáteční bod (0,0),
- mez elasticity (0.01, 300),
- a koncový bod (0.1, 500).
Důležité je aby hodnota napětí zapsaná na druhém řádku odpovídala hodnotě mezního napětí pro elastickou deformaci LIMIT1. V našem případě bude tedy hodnota LIMIT1 = 300 MPa.
Takto zadefinovaný materiál lze použít pro úlohu řešenou v NX Nastran pomocí řešiče SOL 106 pro nelineární statiku nebo pomocí řešiče pro pokročilé nelinearity SOL 601,106.
Definice okrajových podmínek
Definice okrajových podmínek je stejná jako při použití řešiče SOL 101 pro lineární statiku. Pro nelineární statiku (SOL 106) je navíc přidán druhý Subcase, který neobsahuje žádnou sílu a slouží pro simulaci stavu po odlehčení (zobrazení trvalé deformace).
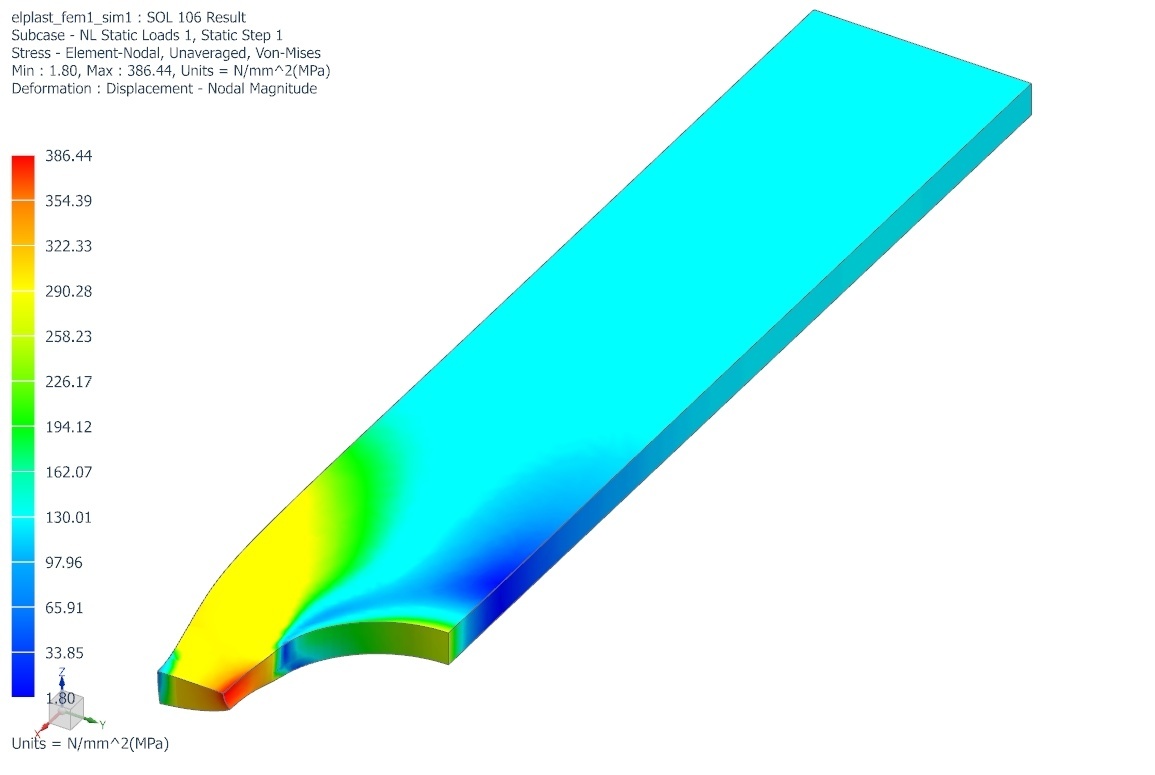
Výsledky úlohy nelineární statiky
Z výsledků je patrný výrazný rozdíl v napětí i deformaci oproti úloze lineární statiky. Celková deformace je dvojnásobná (0,156 mm) a hodnota maximálního napětí je 386 MPa. Z hodnot druhého zátěžného stavu je patrné, že ve vzorku zůstane i po odlehčení trvalá deformace a zbytkové napětí.
V porovnání s výsledky ze SOL 101 nedojde při použití SOL 106 k překročení hodnoty meze pevnosti zvoleného materiálu (500 MPa). Vzorek tedy při jednorázovém zatížení silou 30 kN nepraskne.